|
Hello,
I am a Mechanical and Aerospace PhD candidate in Sylvia Herbert's Safety and Autonomous Systems group at UC San Diego.
willsharpless [at] ucsd [dot] edu / CV / Google Scholar / Github / Linkedin |

|
[Sep 2025 -- I am visiting Chuchu Fan's REALM lab for the fall, would love to grab a coffee if you're in Boston]
|
|
|
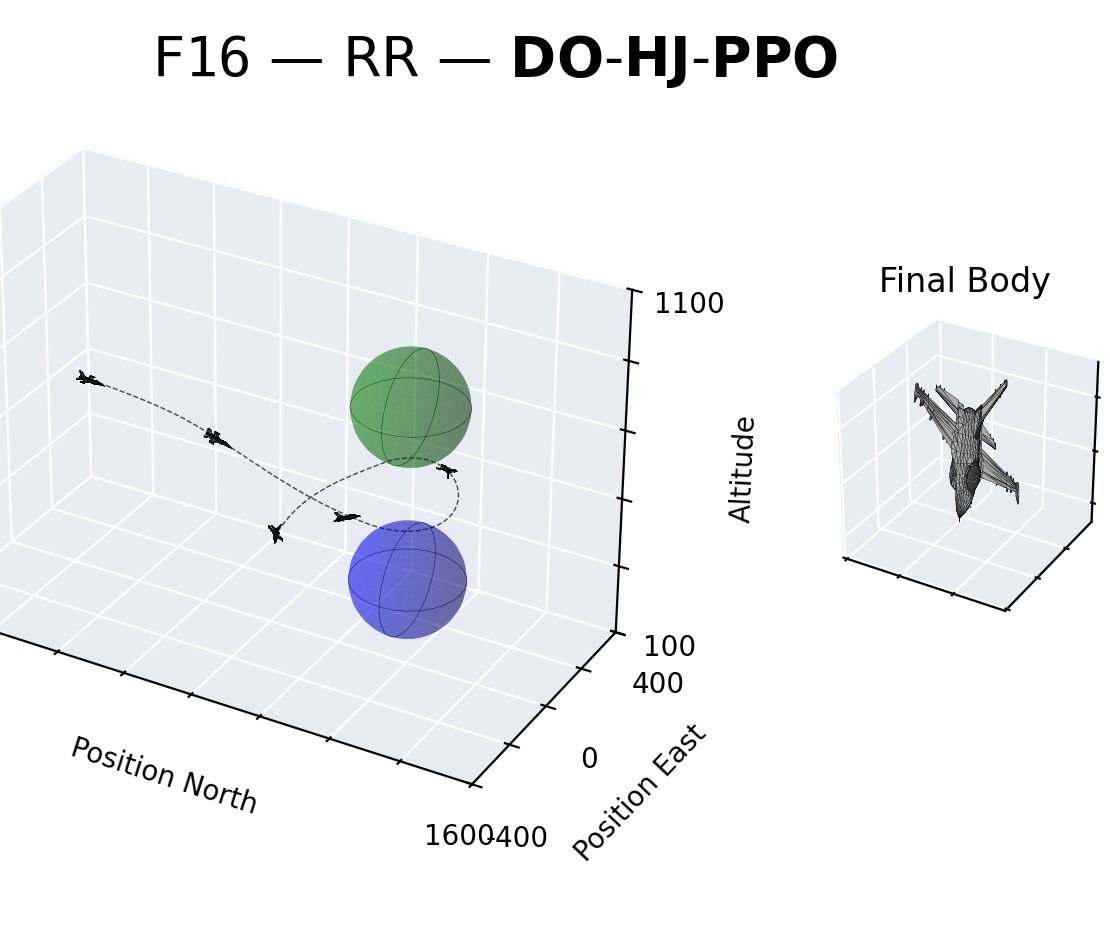
William Sharpless*, Dylan Hirsch*, Sander Tonkens, Nikhil Shinde, Sylvia Herbert. ICLR - September, 2026 Here, we derive novel HJB forms for dual-objective problems (multi-reward or reward & cost) and solve the corresponding Bellman eqns. We use these to design a novel on-policy algorithm (DO-HJ-PPO) which outerperforms STL-RL and CMDP (C-PPO) algorithms for a variety of safe-arrival and multi-achievment tasks. [paper] |
|
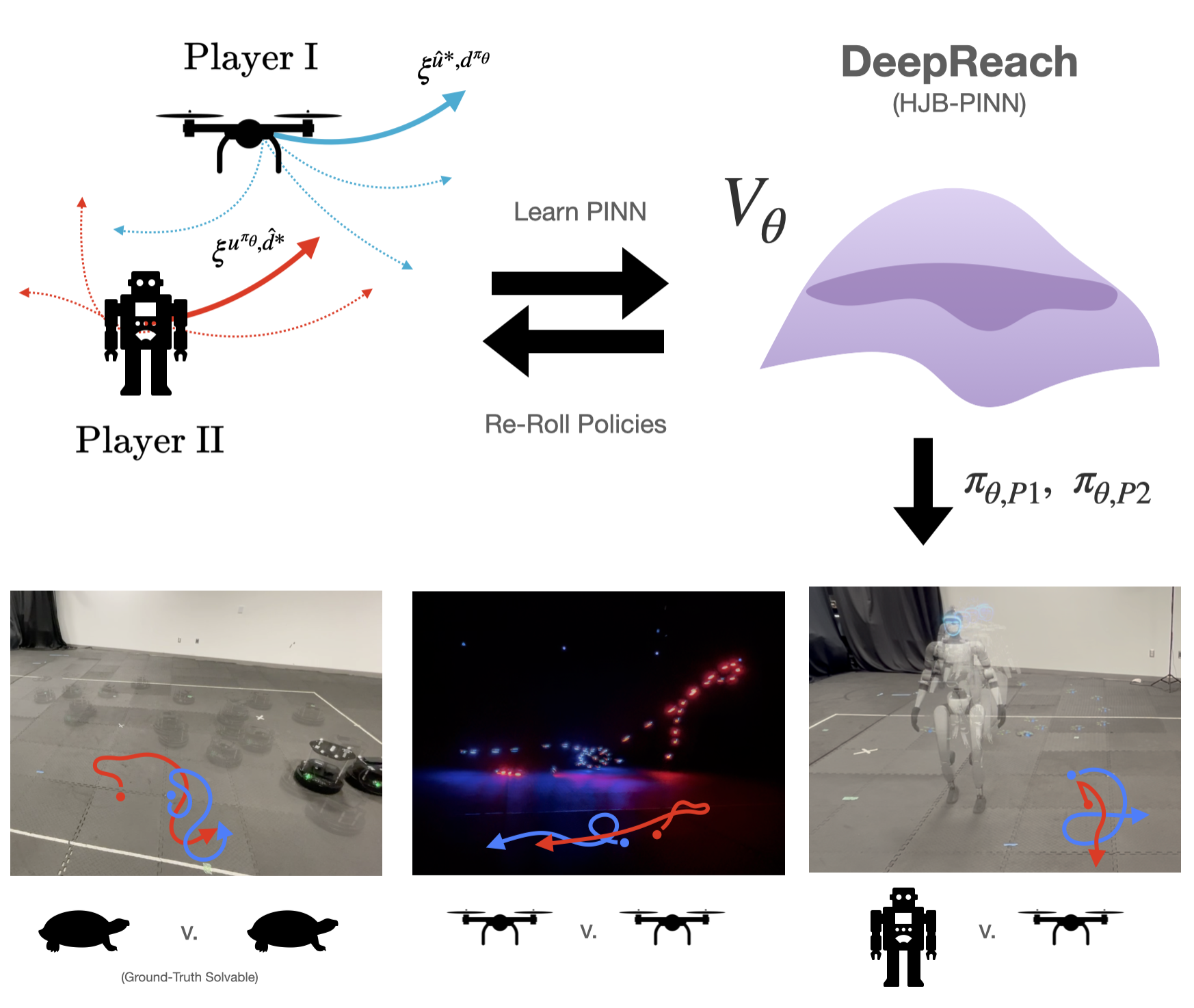
Ryan Teoh, Sander Tonkens, William Sharpless, Aijia Yang, Zeyuan Feng, Somil Bansal, Sylvia Herbert. Recently Submitted - September, 2025 Here, we demonstrate that self-supervised learning of differential game HJ-PDE's, i.e. DeepReach, may be massively improved by active MPC-game supervision, where the opponents policy is defined by the current value approximation. We show that this algorithm is general to a myriad of platforms and robotic agents, namely turtlebots, drones and humanoids. |
|
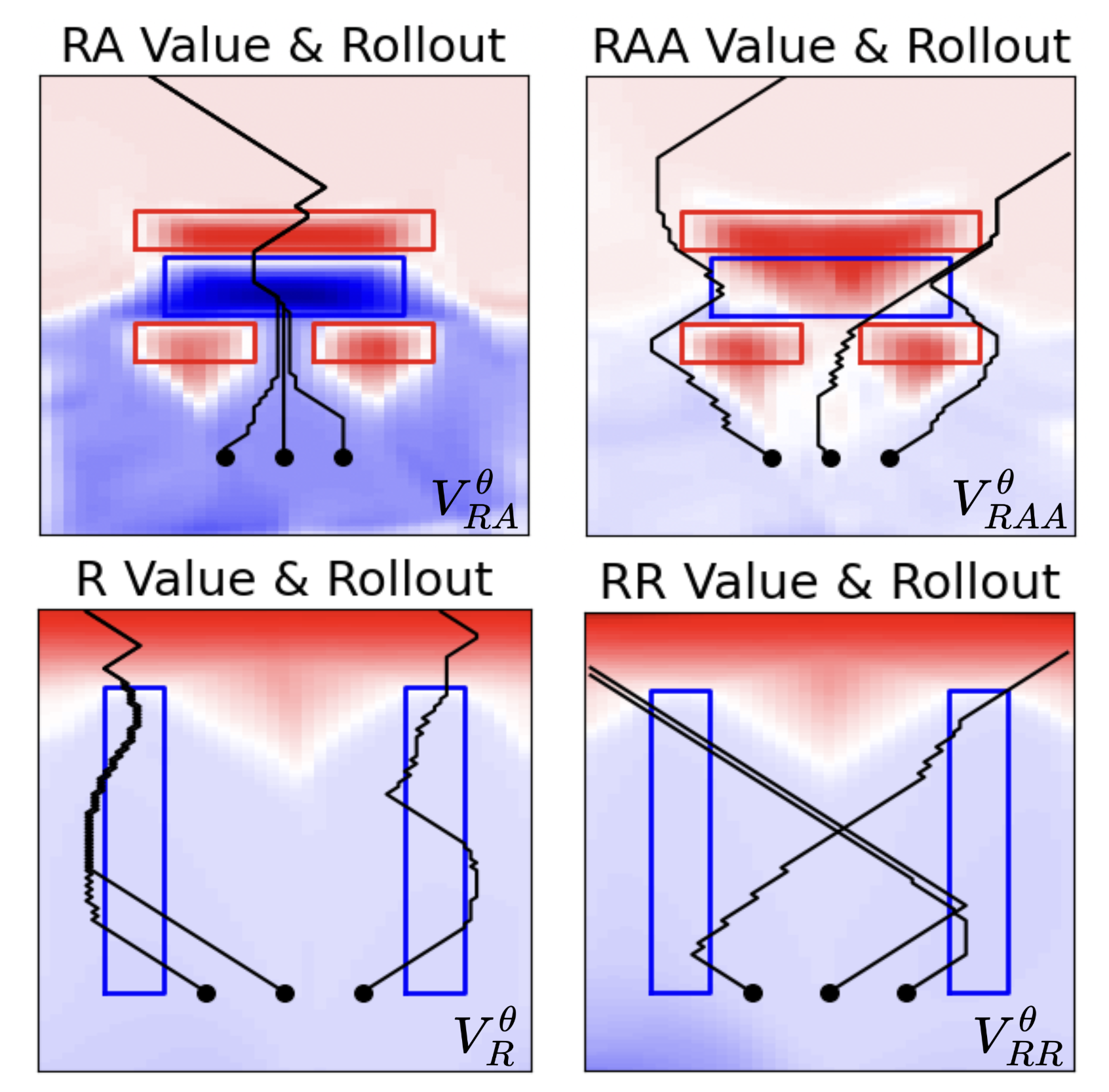
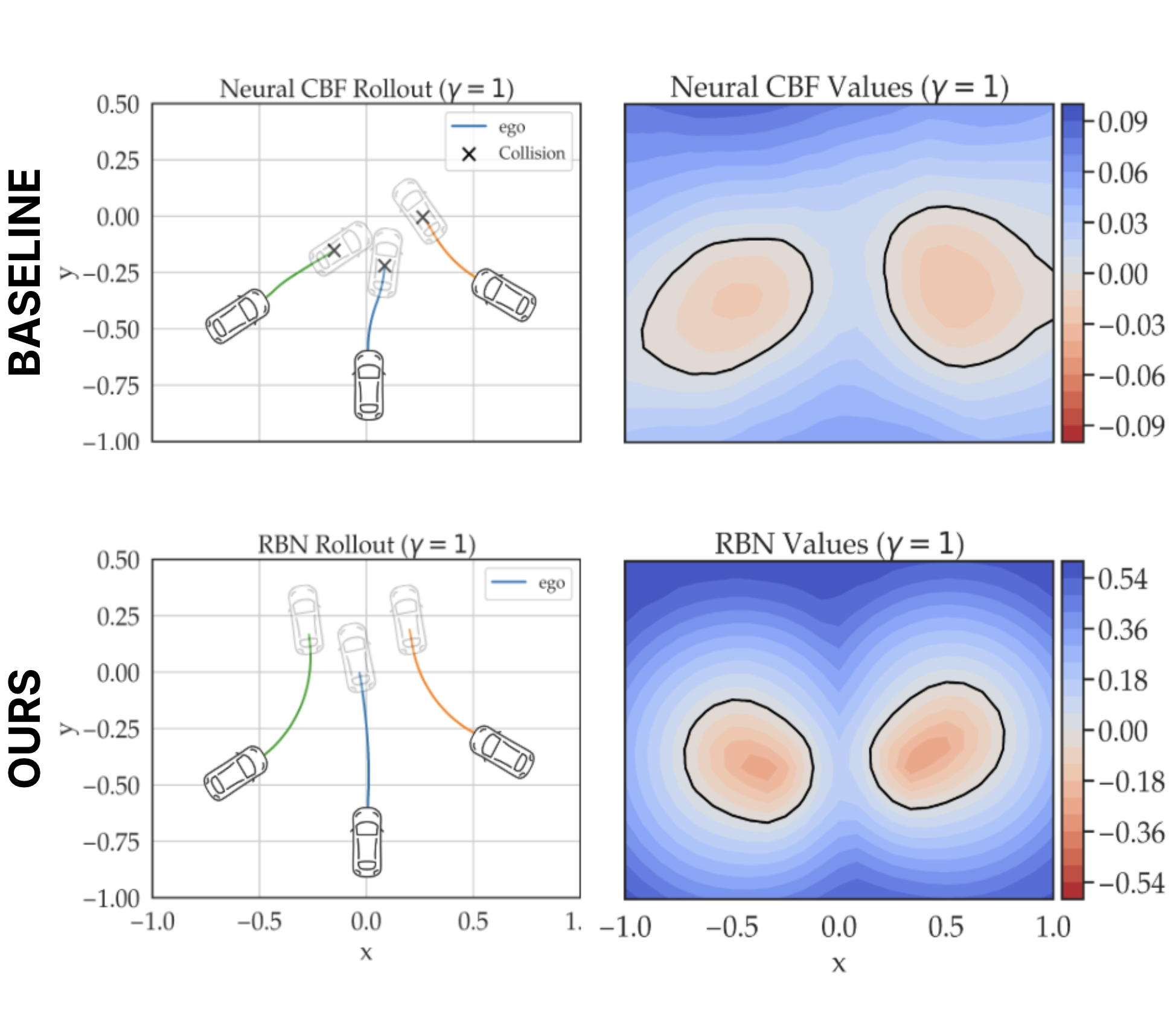
Matthew Kim, William Sharpless, Hyun Joe Jeong, Sander Tonkens, Somil Bansal, Sylvia Herbert. Recently Submitted - April, 2025 In this work, we explore learning smooth, tunable CBF's via the HJB PINN approach, dubbed Reachability Barrier Networks (RBNs). Due to the structure of the problem and uniqueness of the solution, we found RBNs to be more readily learned than neural CBFs, yielding safer appxs. with 5.5x less collisions in a multi-agent experiment. |
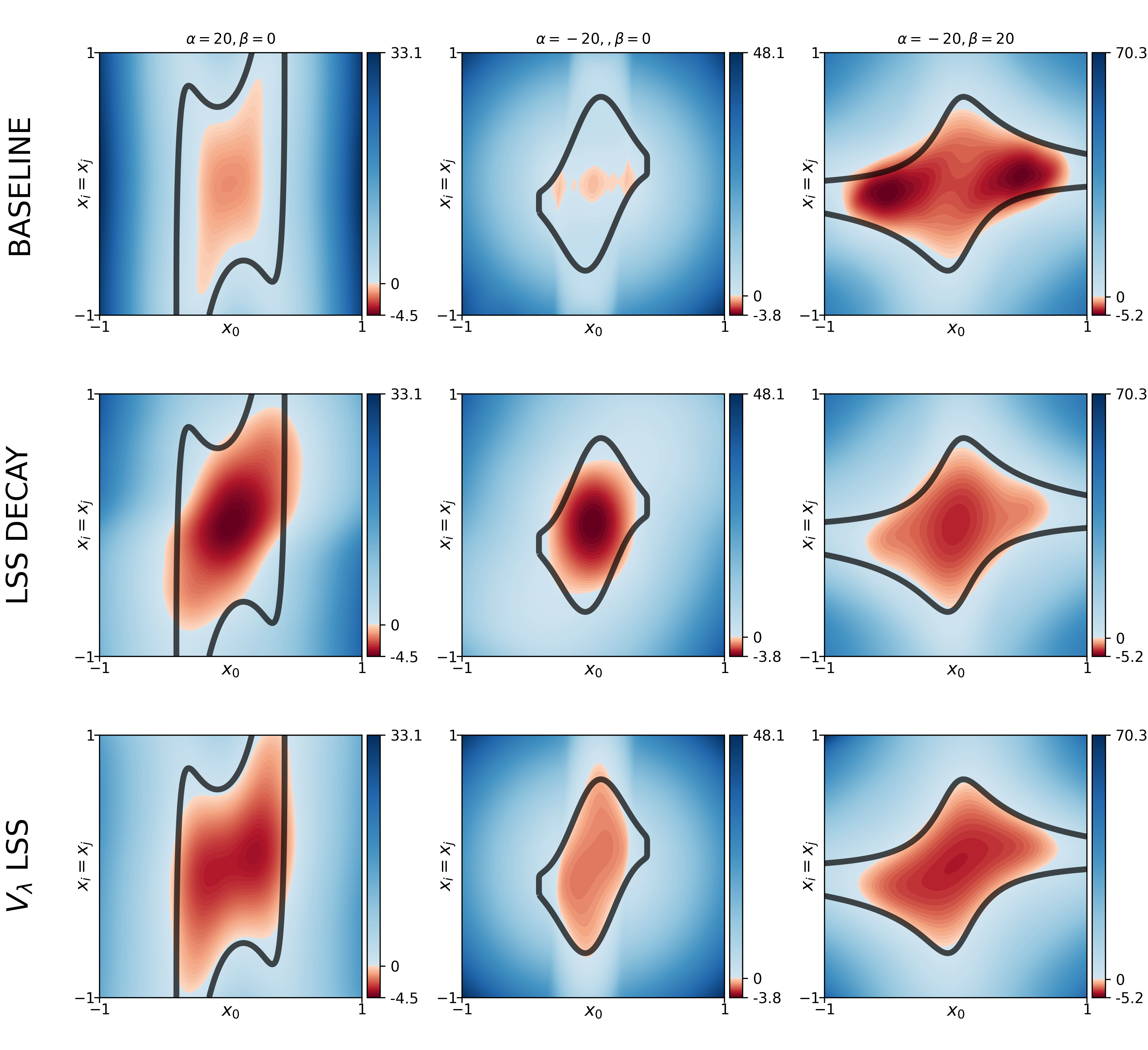 
|
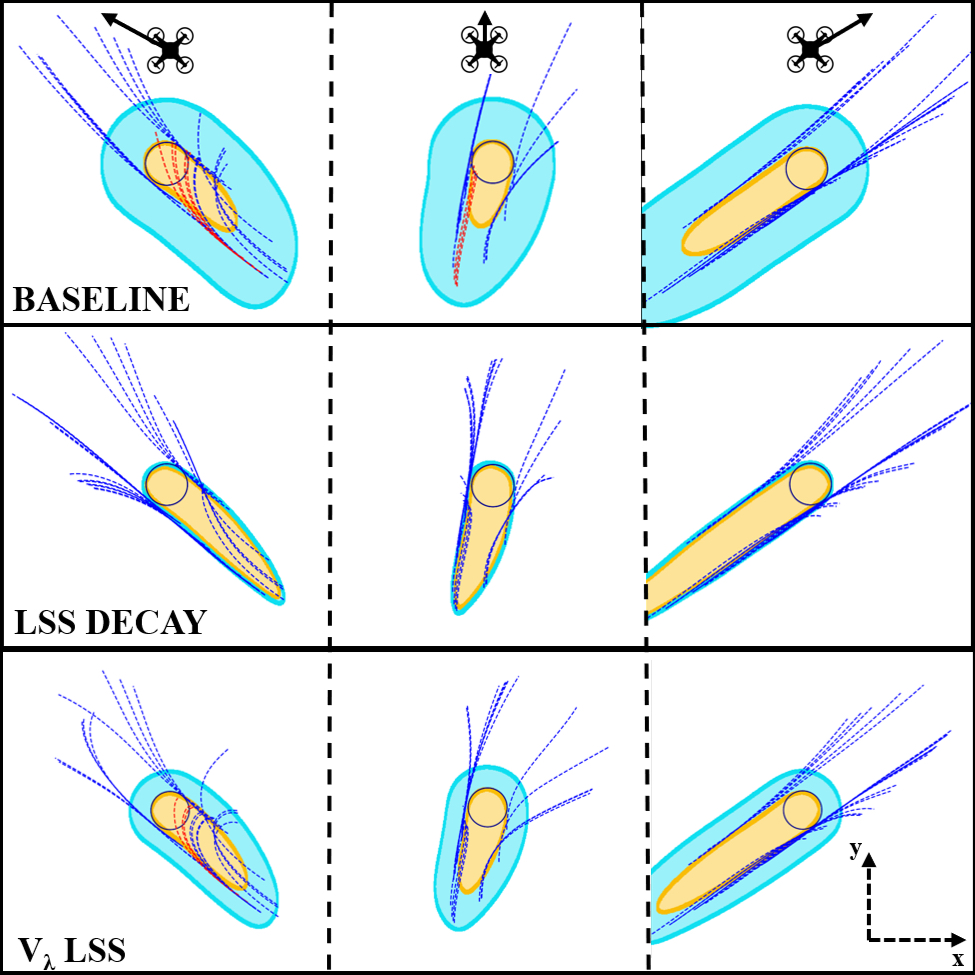
William Sharpless, Zeyuan Feng, Somil Bansal, Sylvia Herbert. Learning for Dynamics & Control - December, 2024 Here, we show that to learn a nonlinear HJ-PDE for autonomy, one may introduce the linear solution for ~25x increase in accuracy and ~20x acceleration in training for problems up to 50-dimensions. [paper] |
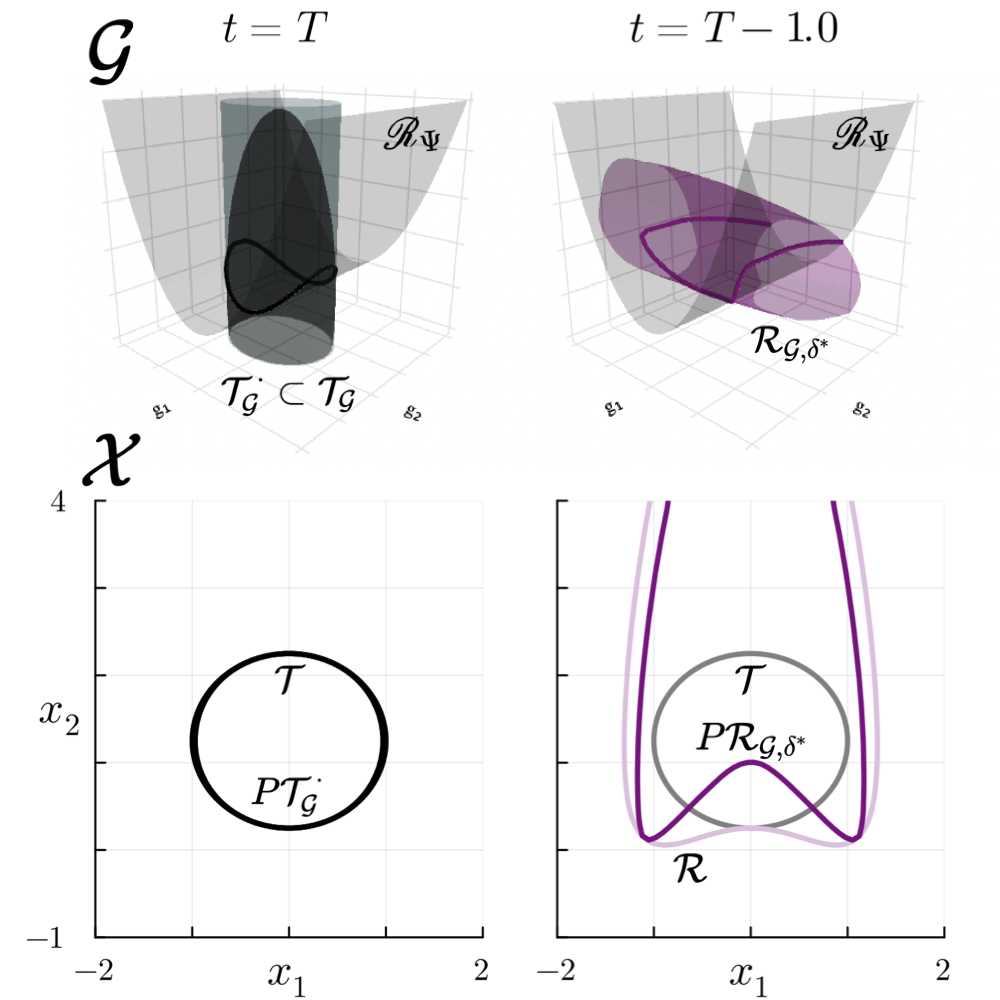 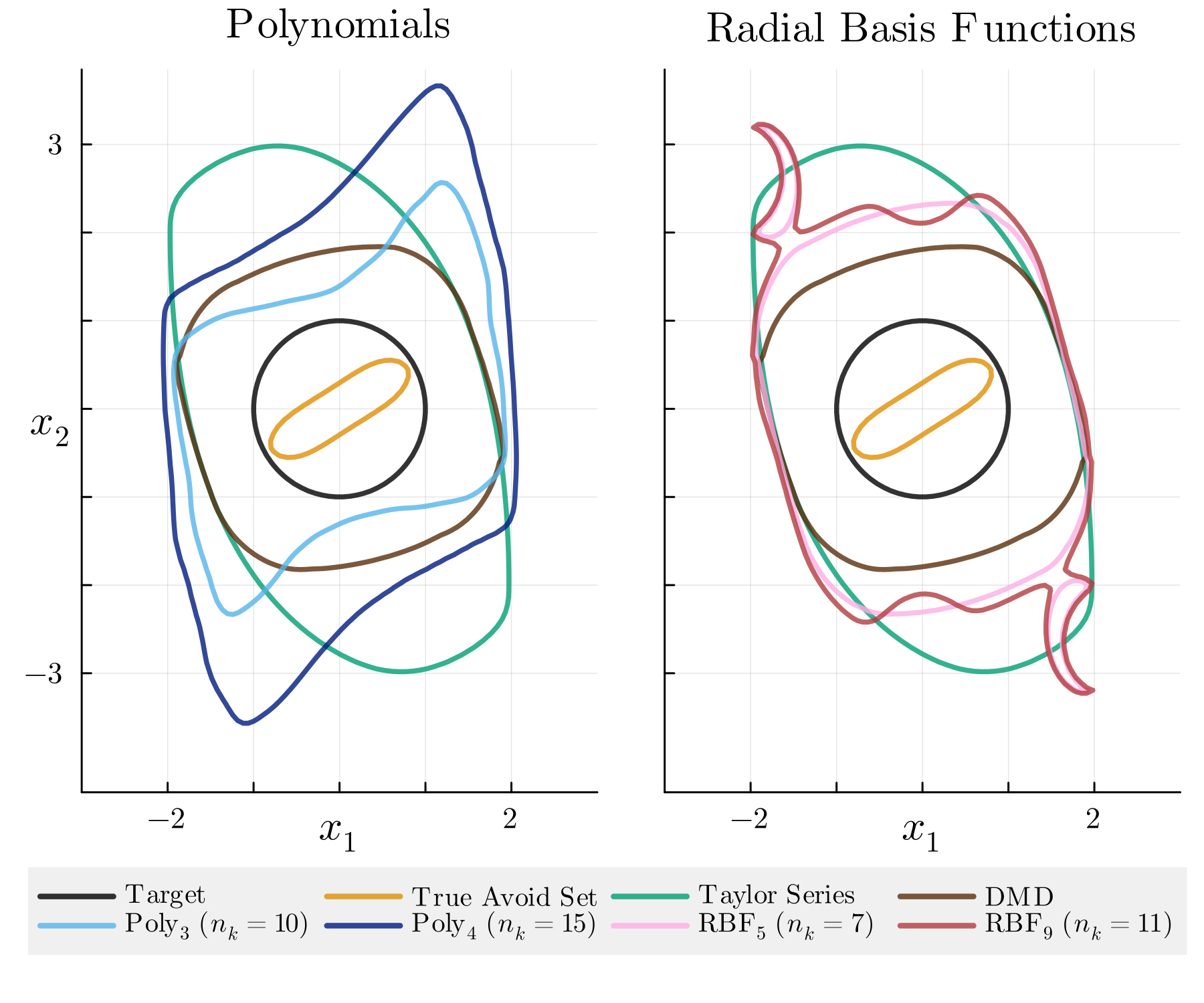
|
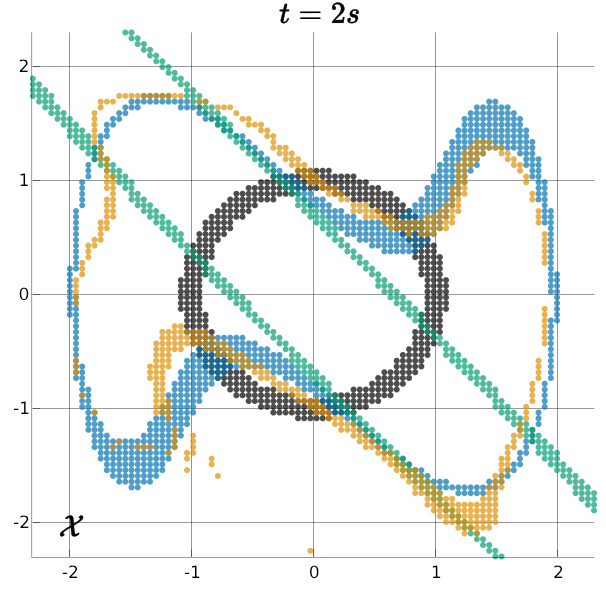
William Sharpless, Yat Tin Chow, Sylvia Herbert. Conference on Decision and Control - March, 2024 Here, we propose a novel, lifted differential game that is guaranteed to be conservative, is solved rapidly, and allows the use of lifting functions such as neural nets, polynomials and radial basis functions to reduce linear error. [paper] |
 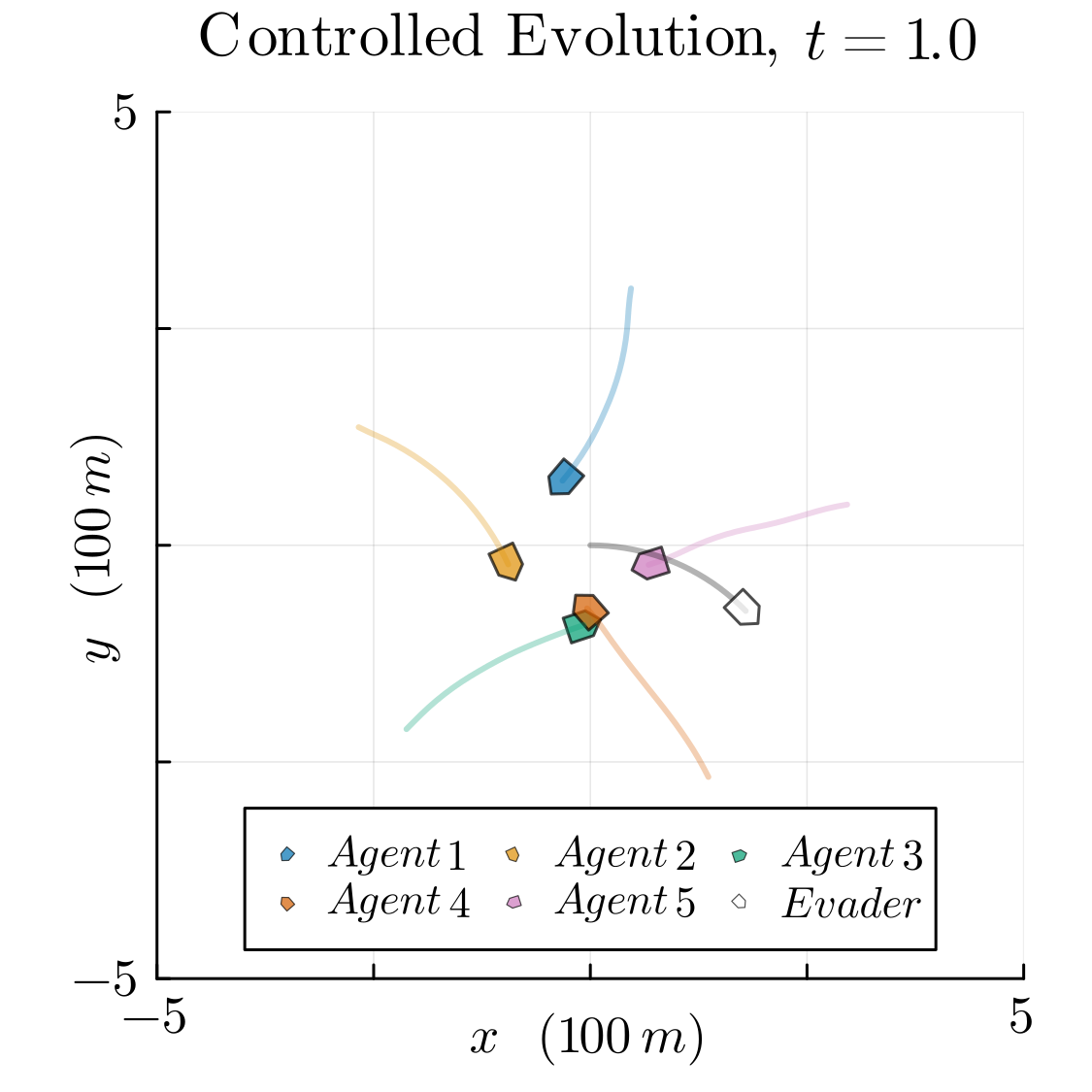
|
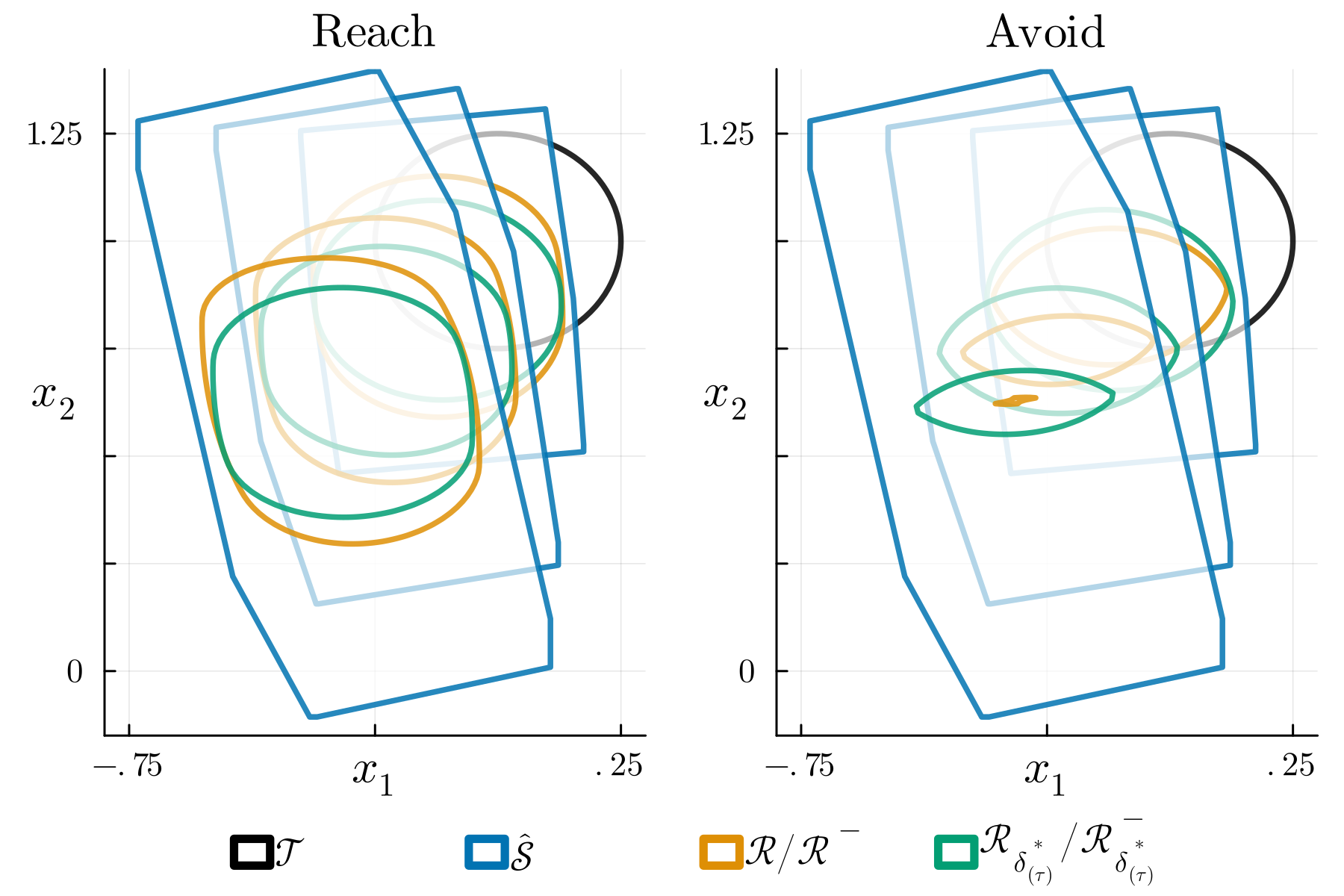
William Sharpless, Yat Tin Chow, Sylvia Herbert. Transactions on Automatic Control - April, 2024 Here, we demonstrate how the error between a nonlinear system of interest and a linearization of it may transformed into an antagonistic player, yielding a conservative linear game that may be solved rapidly in high-dimensions. [paper] |
|
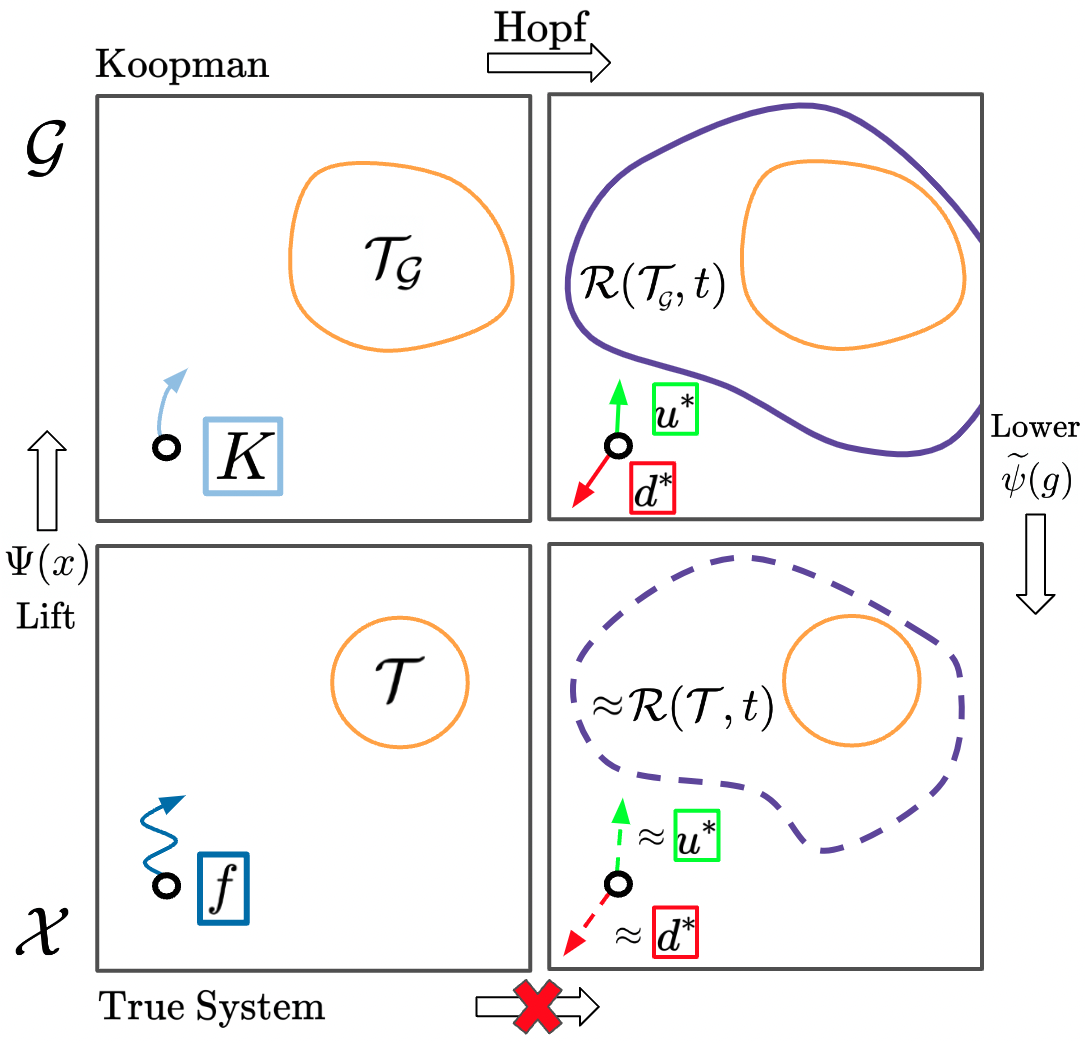
William Sharpless, Nikhil Shinde, Matthew Kim, Yat Tin Chow, Sylvia Herbert. Arxiv (In Review) - November, 2023 In this work, we propose and demonstrate the use of Koopman linearizations to allow the use of the Hopf formula for linear differential games to yield a performant algorithm for high-dimensional, nonlinear autonomy. [paper] |
|
|
|
Semi-autonomous Seminar - UC Berkeley, May 2025 [slides]
Hopf Methods for High-Dimensional HJR |
|
American Math Society (AMS) - Session on Applied Partial Differential Equations, October 2024 [slides]
Lifted Differential Games with Antagonistic Error for Fast, Accurate and Conservative HJB Approximations. |
|
Scientific AI Research Seminar @ Oden Institute - UT Austin, October 2024 [slides]
Lifted Differential Games with Antagonistic Error for Fast, Accurate and Conservative HJB Approximations. |
|
Society of Industrial and Applied Mathematics (SIAM) - High Dimensional Control and HJE Session, September 2024 [slides]
Lifted Differential Games with Antagonistic Error for Fast, Accurate and Conservative HJB Approximations. |
|
Safe and Intelligent Autonomy Seminar @ USC, August 2023 [slides]
Conservative Envelopes with Linear Hopf Solutions for Fast & Safe High-Dimensional Control and Reachability |
|
Level Set Seminar @ UCLA, April 2023 [slides]
Koopman-Hopf Hamilton-Jacobi-Reachability for Fast and Accurate Autonomy |
|
|
|
HopfReachability.jl
Julia software for accelerated non-smooth, convex optimization of the Hopf objective for solving high-dimensional differential games. |
|
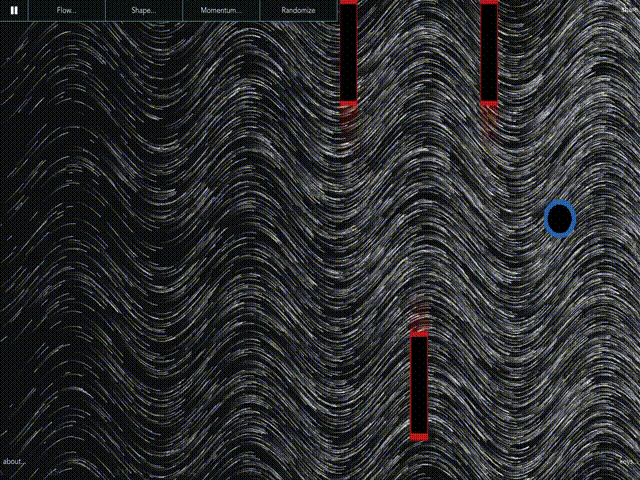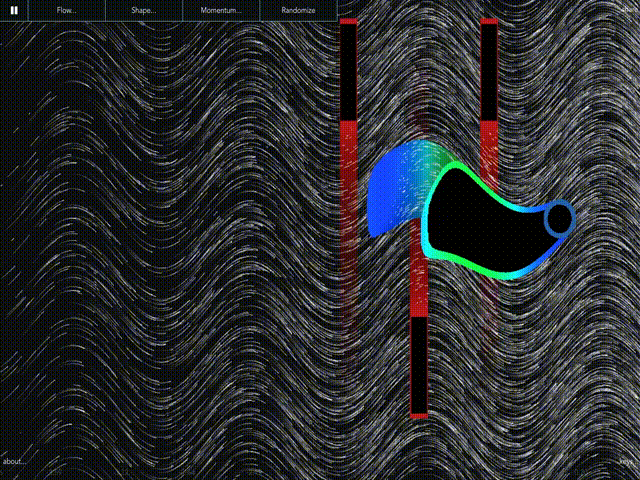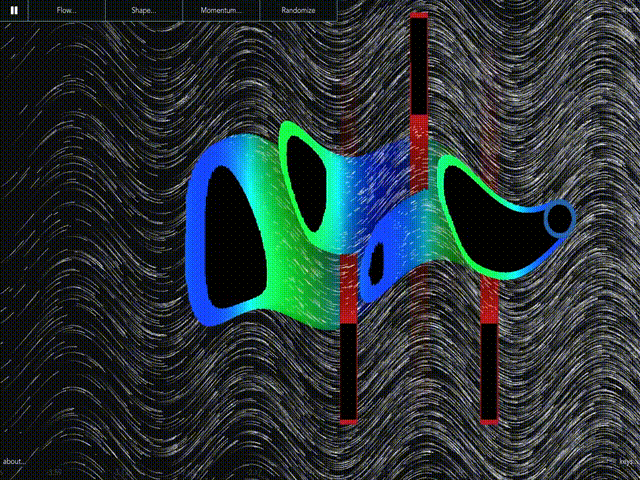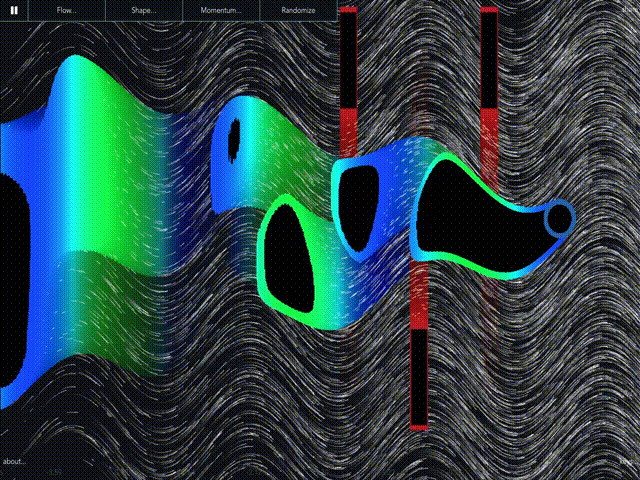
Margo
A fast, interactive level set solver for HJB flows made in GLSL. |
|
Website template by Jon Barron (source code).
|